GraphX プログラミングガイド
概要
GraphX は、Spark におけるグラフおよびグラフ並列計算のための新しいコンポーネントです。全体として、GraphX は Spark の RDD を拡張し、新しい Graph 抽象化を導入します。これは、各頂点とエッジにプロパティが付加された有向マルチグラフです。グラフ計算をサポートするため、GraphX は一連の基本的な演算子(例: subgraph、joinVertices、aggregateMessages)と、最適化された Pregel API のバリアントを提供します。さらに、GraphX には、グラフ分析タスクを簡略化するための、グラフ アルゴリズム と ビルダー のコレクションが増え続けています。
はじめに
開始するには、まず Spark と GraphX をプロジェクトにインポートする必要があります。
import org.apache.spark._
import org.apache.spark.graphx._
// To make some of the examples work we will also need RDD
import org.apache.spark.rdd.RDDSpark シェルを使用しない場合は、SparkContext も必要になります。Spark の開始方法について詳しくは、Spark クイックスタートガイド を参照してください。
プロパティグラフ
プロパティグラフは、ユーザー定義オブジェクトが各頂点とエッジに付加された有向マルチグラフです。有向マルチグラフとは、同じソースおよびデスティネーション頂点を共有する複数の平行エッジを持つ可能性のある有向グラフのことです。平行エッジをサポートする機能は、同じ頂点間に複数の関係(例: 同僚や友人)が存在する可能性のあるシナリオのモデリングを簡略化します。各頂点は、*一意な* 64ビットのロング識別子(VertexId)によってキー付けされます。GraphX は、頂点識別子に順序制約を課しません。同様に、エッジには対応するソースおよびデスティネーション頂点識別子があります。
プロパティグラフは、頂点(VD)とエッジ(ED)の型でパラメータ化されます。これらは、それぞれ頂点とエッジに関連付けられたオブジェクトの型です。
GraphX は、頂点とエッジの型がプリミティブデータ型(例: int、double など)の場合、それらを特殊な配列に格納することで、メモリフットプリントを削減し、表現を最適化します。
場合によっては、同じグラフに異なるプロパティ型を持つ頂点を持たせることが望ましいことがあります。これは、継承を通じて実現できます。たとえば、ユーザーと製品を二部グラフとしてモデル化する場合、次のようなことができます。
class VertexProperty()
case class UserProperty(val name: String) extends VertexProperty
case class ProductProperty(val name: String, val price: Double) extends VertexProperty
// The graph might then have the type:
var graph: Graph[VertexProperty, String] = nullRDD と同様に、プロパティグラフは不変、分散、および耐障害性があります。グラフの値や構造の変更は、目的の変更を生成する新しいグラフを作成することによって行われます。元のグラフの大部分(つまり、影響を受けない構造、属性、インデックス)は、新しいグラフで再利用され、この本質的に関数的なデータ構造のコストを削減します。グラフは、頂点パーティショニングヒューリスティクスの範囲を通じてエグゼキュータ全体にパーティション分割されます。RDD と同様に、障害が発生した場合でも、グラフの各パーティションは別のマシンで再作成できます。
論理的には、プロパティグラフは、各頂点とエッジのプロパティをエンコードする型付けされたコレクション(RDD)のペアに対応します。その結果、Graph クラスには、グラフの頂点とエッジにアクセスするためのメンバーが含まれています。
class Graph[VD, ED] {
val vertices: VertexRDD[VD]
val edges: EdgeRDD[ED]
}クラス VertexRDD[VD] と EdgeRDD[ED] は、それぞれ RDD[(VertexId, VD)] と RDD[Edge[ED]] の拡張および最適化されたバージョンです。どちらの VertexRDD[VD] と EdgeRDD[ED] も、グラフ計算を中心に構築された追加機能を提供し、内部最適化を活用します。頂点とエッジ RDD のセクションで VertexRDDVertexRDD と EdgeRDDEdgeRDD API について詳しく説明しますが、現時点では、それらを単に RDD[(VertexId, VD)] および RDD[Edge[ED]] の形式の RDD として考えることができます。
プロパティグラフの例
GraphX プロジェクトのさまざまな共同作業者で構成されるプロパティグラフを構築したいとします。頂点プロパティにはユーザー名と職業を含めることができます。エッジには、共同作業者間の関係を説明する文字列を注釈付けできます。
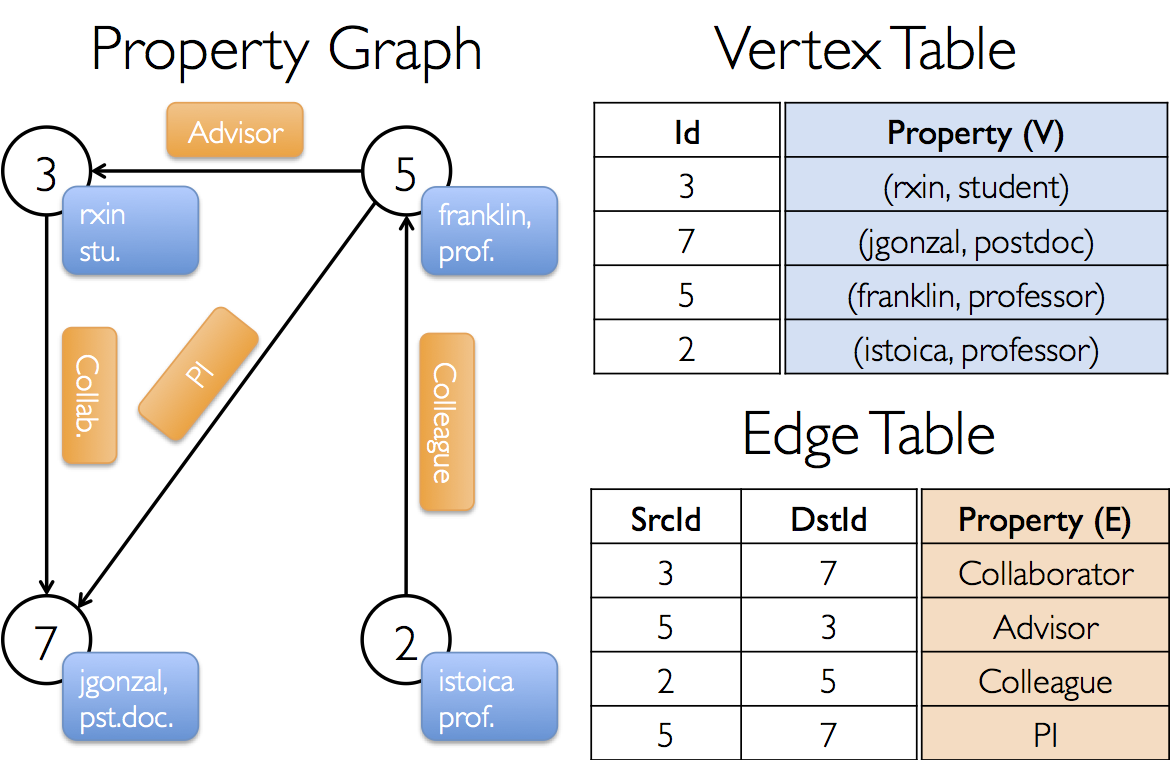
結果のグラフの型シグネチャは次のようになります。
val userGraph: Graph[(String, String), String]生のファイル、RDD、さらには合成ジェネレーターからプロパティグラフを構築するには多数の方法があり、これらは グラフビルダー のセクションでさらに詳しく説明されています。おそらく最も一般的な方法は、Graph オブジェクト を使用することです。たとえば、次のコードは RDD のコレクションからグラフを構築します。
// Assume the SparkContext has already been constructed
val sc: SparkContext
// Create an RDD for the vertices
val users: RDD[(VertexId, (String, String))] =
sc.parallelize(Seq((3L, ("rxin", "student")), (7L, ("jgonzal", "postdoc")),
(5L, ("franklin", "prof")), (2L, ("istoica", "prof"))))
// Create an RDD for edges
val relationships: RDD[Edge[String]] =
sc.parallelize(Seq(Edge(3L, 7L, "collab"), Edge(5L, 3L, "advisor"),
Edge(2L, 5L, "colleague"), Edge(5L, 7L, "pi")))
// Define a default user in case there are relationship with missing user
val defaultUser = ("John Doe", "Missing")
// Build the initial Graph
val graph = Graph(users, relationships, defaultUser)上記の例では、Edge ケースクラスを使用しています。エッジには、ソースおよびデスティネーション頂点識別子に対応する srcId と dstId があります。さらに、Edge クラスには、エッジプロパティを格納する attr メンバーがあります。
それぞれ graph.vertices および graph.edges メンバーを使用して、グラフを対応する頂点ビューとエッジビューに分解できます。
val graph: Graph[(String, String), String] // Constructed from above
// Count all users which are postdocs
graph.vertices.filter { case (id, (name, pos)) => pos == "postdoc" }.count
// Count all the edges where src > dst
graph.edges.filter(e => e.srcId > e.dstId).count
graph.verticesはRDD[(VertexId, (String, String))]を拡張するVertexRDD[(String, String)]を返すため、scala のcase式を使用してタプルを分解します。一方、graph.edgesはEdge[String]オブジェクトを含むEdgeRDDを返します。次のように、ケースクラスの型コンストラクタを使用することもできました。
graph.edges.filter { case Edge(src, dst, prop) => src > dst }.countプロパティグラフの頂点およびエッジビューに加えて、GraphX はトリプレットビューも公開します。トリプレットビューは、論理的に頂点およびエッジのプロパティを結合し、EdgeTriplet クラスのインスタンスを含む RDD[EdgeTriplet[VD, ED]] を生成します。この*結合*は、次の SQL 式で表現できます。
SELECT src.id, dst.id, src.attr, e.attr, dst.attr
FROM edges AS e LEFT JOIN vertices AS src, vertices AS dst
ON e.srcId = src.Id AND e.dstId = dst.Idまたは、グラフで次のように表すことができます。

EdgeTriplet クラスは Edge クラスを拡張し、それぞれソースおよびデスティネーションプロパティを含む srcAttr および dstAttr メンバーを追加します。グラフのトリプレットビューを使用して、ユーザー間の関係を説明する文字列のコレクションをレンダリングできます。
val graph: Graph[(String, String), String] // Constructed from above
// Use the triplets view to create an RDD of facts.
val facts: RDD[String] =
graph.triplets.map(triplet =>
triplet.srcAttr._1 + " is the " + triplet.attr + " of " + triplet.dstAttr._1)
facts.collect.foreach(println(_))グラフ演算子
RDD には map、filter、reduceByKey のような基本的な操作があるのと同様に、プロパティグラフにも、ユーザー定義関数を受け取り、変換されたプロパティと構造を持つ新しいグラフを生成する基本的な演算子のコレクションがあります。最適化された実装を持つコア演算子は Graph で定義されており、コア演算子の合成として表現される便利な演算子は GraphOps で定義されています。ただし、Scala の暗黙の型変換により、GraphOps の演算子は Graph のメンバーとして自動的に利用可能になります。たとえば、次の方法で各頂点の入次数を計算できます(GraphOps で定義)。
val graph: Graph[(String, String), String]
// Use the implicit GraphOps.inDegrees operator
val inDegrees: VertexRDD[Int] = graph.inDegreesコアグラフ操作と GraphOps を区別する理由は、将来的に異なるグラフ表現をサポートできるようにするためです。各グラフ表現は、コア操作の実装を提供し、GraphOps で定義されている多くの便利な操作を再利用する必要があります。
演算子一覧
以下は、Graph と GraphOps の両方で定義されている機能の簡単な概要ですが、簡単にするために Graph のメンバーとして提示されています。一部の関数シグネチャは簡略化されており(例: デフォルト引数と型制約は削除)、より高度な機能は削除されているため、操作の公式リストについては API ドキュメントを参照してください。
/** Summary of the functionality in the property graph */
class Graph[VD, ED] {
// Information about the Graph ===================================================================
val numEdges: Long
val numVertices: Long
val inDegrees: VertexRDD[Int]
val outDegrees: VertexRDD[Int]
val degrees: VertexRDD[Int]
// Views of the graph as collections =============================================================
val vertices: VertexRDD[VD]
val edges: EdgeRDD[ED]
val triplets: RDD[EdgeTriplet[VD, ED]]
// Functions for caching graphs ==================================================================
def persist(newLevel: StorageLevel = StorageLevel.MEMORY_ONLY): Graph[VD, ED]
def cache(): Graph[VD, ED]
def unpersistVertices(blocking: Boolean = false): Graph[VD, ED]
// Change the partitioning heuristic ============================================================
def partitionBy(partitionStrategy: PartitionStrategy): Graph[VD, ED]
// Transform vertex and edge attributes ==========================================================
def mapVertices[VD2](map: (VertexId, VD) => VD2): Graph[VD2, ED]
def mapEdges[ED2](map: Edge[ED] => ED2): Graph[VD, ED2]
def mapEdges[ED2](map: (PartitionID, Iterator[Edge[ED]]) => Iterator[ED2]): Graph[VD, ED2]
def mapTriplets[ED2](map: EdgeTriplet[VD, ED] => ED2): Graph[VD, ED2]
def mapTriplets[ED2](map: (PartitionID, Iterator[EdgeTriplet[VD, ED]]) => Iterator[ED2])
: Graph[VD, ED2]
// Modify the graph structure ====================================================================
def reverse: Graph[VD, ED]
def subgraph(
epred: EdgeTriplet[VD,ED] => Boolean = (x => true),
vpred: (VertexId, VD) => Boolean = ((v, d) => true))
: Graph[VD, ED]
def mask[VD2, ED2](other: Graph[VD2, ED2]): Graph[VD, ED]
def groupEdges(merge: (ED, ED) => ED): Graph[VD, ED]
// Join RDDs with the graph ======================================================================
def joinVertices[U](table: RDD[(VertexId, U)])(mapFunc: (VertexId, VD, U) => VD): Graph[VD, ED]
def outerJoinVertices[U, VD2](other: RDD[(VertexId, U)])
(mapFunc: (VertexId, VD, Option[U]) => VD2)
: Graph[VD2, ED]
// Aggregate information about adjacent triplets =================================================
def collectNeighborIds(edgeDirection: EdgeDirection): VertexRDD[Array[VertexId]]
def collectNeighbors(edgeDirection: EdgeDirection): VertexRDD[Array[(VertexId, VD)]]
def aggregateMessages[Msg: ClassTag](
sendMsg: EdgeContext[VD, ED, Msg] => Unit,
mergeMsg: (Msg, Msg) => Msg,
tripletFields: TripletFields = TripletFields.All)
: VertexRDD[A]
// Iterative graph-parallel computation ==========================================================
def pregel[A](initialMsg: A, maxIterations: Int, activeDirection: EdgeDirection)(
vprog: (VertexId, VD, A) => VD,
sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexId, A)],
mergeMsg: (A, A) => A)
: Graph[VD, ED]
// Basic graph algorithms ========================================================================
def pageRank(tol: Double, resetProb: Double = 0.15): Graph[Double, Double]
def connectedComponents(): Graph[VertexId, ED]
def triangleCount(): Graph[Int, ED]
def stronglyConnectedComponents(numIter: Int): Graph[VertexId, ED]
}プロパティ演算子
RDD の map 演算子と同様に、プロパティグラフには次のものが含まれます。
class Graph[VD, ED] {
def mapVertices[VD2](map: (VertexId, VD) => VD2): Graph[VD2, ED]
def mapEdges[ED2](map: Edge[ED] => ED2): Graph[VD, ED2]
def mapTriplets[ED2](map: EdgeTriplet[VD, ED] => ED2): Graph[VD, ED2]
}これらの演算子のそれぞれは、ユーザー定義の map 関数によって頂点またはエッジのプロパティが変更された新しいグラフを生成します。
この場合、グラフ構造は影響を受けないことに注意してください。これは、これらの演算子の重要な特徴であり、結果のグラフが元のグラフの構造インデックスを再利用できるようにします。次のスニペットは論理的に同等ですが、最初のスニペットは構造インデックスを保持せず、GraphX システムの最適化の恩恵を受けません。
val newVertices = graph.vertices.map { case (id, attr) => (id, mapUdf(id, attr)) }
val newGraph = Graph(newVertices, graph.edges)代わりに、インデックスを保持するために
mapVerticesを使用します。
val newGraph = graph.mapVertices((id, attr) => mapUdf(id, attr))これらの演算子は、特定の計算のためにグラフを初期化したり、不要なプロパティを投影したりするためによく使用されます。たとえば、頂点プロパティとして出次数を持つグラフ(このようなグラフの構築方法については後述)があると、PageRank のために初期化します。
// Given a graph where the vertex property is the out degree
val inputGraph: Graph[Int, String] =
graph.outerJoinVertices(graph.outDegrees)((vid, _, degOpt) => degOpt.getOrElse(0))
// Construct a graph where each edge contains the weight
// and each vertex is the initial PageRank
val outputGraph: Graph[Double, Double] =
inputGraph.mapTriplets(triplet => 1.0 / triplet.srcAttr).mapVertices((id, _) => 1.0)構造演算子
現在、GraphX は一般的に使用される構造演算子の単純なセットのみをサポートしており、将来的にはさらに追加する予定です。以下は、基本的な構造演算子のリストです。
class Graph[VD, ED] {
def reverse: Graph[VD, ED]
def subgraph(epred: EdgeTriplet[VD,ED] => Boolean,
vpred: (VertexId, VD) => Boolean): Graph[VD, ED]
def mask[VD2, ED2](other: Graph[VD2, ED2]): Graph[VD, ED]
def groupEdges(merge: (ED, ED) => ED): Graph[VD,ED]
}reverse 演算子は、すべてのエッジの方向を反転した新しいグラフを返します。これは、たとえば逆 PageRank を計算しようとする場合に役立ちます。reverse 操作は頂点またはエッジのプロパティを変更せず、エッジの数を変更しないため、データ移動や重複なしに効率的に実装できます。
subgraph 演算子は、頂点述語とエッジ述語を受け取り、頂点述語を満たす(true を評価する)頂点のみと、エッジ述語を満たし*、かつ頂点述語を満たす頂点に接続する*エッジのみを含むグラフを返します。 subgraph 演算子は、グラフを関心のある頂点とエッジに制限したり、壊れたリンクを削除したりするなど、さまざまな状況で使用できます。たとえば、次のコードでは壊れたリンクを削除します。
// Create an RDD for the vertices
val users: RDD[(VertexId, (String, String))] =
sc.parallelize(Seq((3L, ("rxin", "student")), (7L, ("jgonzal", "postdoc")),
(5L, ("franklin", "prof")), (2L, ("istoica", "prof")),
(4L, ("peter", "student"))))
// Create an RDD for edges
val relationships: RDD[Edge[String]] =
sc.parallelize(Seq(Edge(3L, 7L, "collab"), Edge(5L, 3L, "advisor"),
Edge(2L, 5L, "colleague"), Edge(5L, 7L, "pi"),
Edge(4L, 0L, "student"), Edge(5L, 0L, "colleague")))
// Define a default user in case there are relationship with missing user
val defaultUser = ("John Doe", "Missing")
// Build the initial Graph
val graph = Graph(users, relationships, defaultUser)
// Notice that there is a user 0 (for which we have no information) connected to users
// 4 (peter) and 5 (franklin).
graph.triplets.map(
triplet => triplet.srcAttr._1 + " is the " + triplet.attr + " of " + triplet.dstAttr._1
).collect.foreach(println(_))
// Remove missing vertices as well as the edges to connected to them
val validGraph = graph.subgraph(vpred = (id, attr) => attr._2 != "Missing")
// The valid subgraph will disconnect users 4 and 5 by removing user 0
validGraph.vertices.collect.foreach(println(_))
validGraph.triplets.map(
triplet => triplet.srcAttr._1 + " is the " + triplet.attr + " of " + triplet.dstAttr._1
).collect.foreach(println(_))上記の例では、頂点述語のみが提供されていることに注意してください。頂点述語またはエッジ述語が提供されていない場合、
subgraph演算子のデフォルトはtrueです。
mask 演算子は、入力グラフにも存在する頂点とエッジを含むグラフを返すことによってサブグラフを構築します。これは、subgraph 演算子と組み合わせて、別の関連グラフのプロパティに基づいてグラフを制限するために使用できます。たとえば、欠落している頂点を持つグラフを使用して連結成分を実行し、その後、有効なサブグラフに結果を制限することができます。
// Run Connected Components
val ccGraph = graph.connectedComponents() // No longer contains missing field
// Remove missing vertices as well as the edges to connected to them
val validGraph = graph.subgraph(vpred = (id, attr) => attr._2 != "Missing")
// Restrict the answer to the valid subgraph
val validCCGraph = ccGraph.mask(validGraph)groupEdges 演算子は、マルチグラフ内の平行エッジ(つまり、頂点のペア間の重複エッジ)をマージします。多くの数値アプリケーションでは、平行エッジを*加算*(重みを結合)して単一のエッジにすることで、グラフのサイズを削減できます。
結合演算子
多くの場合、外部コレクション(RDD)からのデータをグラフに結合する必要があります。たとえば、既存のグラフにマージしたい追加のユーザープロパティがある場合や、一方のグラフからもう一方のグラフに頂点プロパティをプルしたい場合があります。これらのタスクは、*結合*演算子を使用して実行できます。以下に、主要な結合演算子を示します。
class Graph[VD, ED] {
def joinVertices[U](table: RDD[(VertexId, U)])(map: (VertexId, VD, U) => VD)
: Graph[VD, ED]
def outerJoinVertices[U, VD2](table: RDD[(VertexId, U)])(map: (VertexId, VD, Option[U]) => VD2)
: Graph[VD2, ED]
}joinVertices 演算子は、頂点と入力 RDD を結合し、結合された頂点の結果にユーザー定義の map 関数を適用して取得した頂点プロパティを持つ新しいグラフを返します。RDD に一致する値がない頂点は、元の値を保持します。
RDD に指定された頂点に対して複数の値が含まれている場合、1 つの値のみが使用されることに注意してください。したがって、入力 RDD を次を使用して一意にすることをお勧めします。これにより、結果の値が*事前インデックス付け*され、後続の結合が大幅に高速化されます。
val nonUniqueCosts: RDD[(VertexId, Double)]
val uniqueCosts: VertexRDD[Double] =
graph.vertices.aggregateUsingIndex(nonUnique, (a,b) => a + b)
val joinedGraph = graph.joinVertices(uniqueCosts)(
(id, oldCost, extraCost) => oldCost + extraCost)より汎用的な outerJoinVertices は joinVertices と同様に動作しますが、ユーザー定義の map 関数がすべての頂点に適用され、頂点プロパティ型を変更できる点が異なります。すべての頂点に入力 RDD と一致する値がない可能性があるため、map 関数は Option 型を取ります。たとえば、PageRank のためにグラフを設定し、頂点プロパティを outDegree で初期化できます。
val outDegrees: VertexRDD[Int] = graph.outDegrees
val degreeGraph = graph.outerJoinVertices(outDegrees) { (id, oldAttr, outDegOpt) =>
outDegOpt match {
case Some(outDeg) => outDeg
case None => 0 // No outDegree means zero outDegree
}
}上記の例で使用されている複数の引数リスト(例:
f(a)(b))のカリー化関数パターンに気付いたかもしれません。f(a)(b)をf(a,b)と記述することもできましたが、これはbの型推論がaに依存しないことを意味します。その結果、ユーザーはユーザー定義関数の型注釈を提供する必要があります。
val joinedGraph = graph.joinVertices(uniqueCosts,
(id: VertexId, oldCost: Double, extraCost: Double) => oldCost + extraCost)近傍集計
多くのグラフ分析タスクの重要なステップは、各頂点の近傍に関する情報を集計することです。たとえば、各ユーザーが何人のフォロワーがいるか、または各ユーザーのフォロワーの平均年齢を知りたい場合があります。多くの反復グラフアルゴリズム(例: PageRank、最短経路、連結成分)は、隣接頂点のプロパティ(例: 現在の PageRank 値、ソースまでの最短経路、到達可能な最小頂点 ID)を繰り返し集計します。
パフォーマンスを向上させるため、主要な集計演算子は
graph.mapReduceTripletsから新しいgraph.AggregateMessagesに変更されました。API の変更は比較的小さいですが、以下に移行ガイドを提供します。
メッセージ集計 (aggregateMessages)
GraphX のコア集計操作は aggregateMessages です。この演算子は、ユーザー定義の sendMsg 関数をグラフ内の各*エッジトリプレット*に適用し、その後 mergeMsg 関数を使用してそれらのメッセージをデスティネーション頂点で集計します。
class Graph[VD, ED] {
def aggregateMessages[Msg: ClassTag](
sendMsg: EdgeContext[VD, ED, Msg] => Unit,
mergeMsg: (Msg, Msg) => Msg,
tripletFields: TripletFields = TripletFields.All)
: VertexRDD[Msg]
}ユーザー定義の sendMsg 関数は EdgeContext を受け取ります。これは、ソースおよびデスティネーション属性をエッジ属性とともに公開し、ソースおよびデスティネーション属性にメッセージを送信するための関数(sendToSrc および sendToDst)を提供します。 sendMsg を map-reduce の*map* 関数と考えることができます。ユーザー定義の mergeMsg 関数は、同じ頂点に宛てられた 2 つのメッセージを受け取り、1 つのメッセージを生成します。 mergeMsg を map-reduce の*reduce* 関数と考えることができます。aggregateMessages 演算子は、各頂点に宛てられた集計メッセージ(Msg 型)を含む VertexRDD[Msg] を返します。メッセージを受信しなかった頂点は、返される VertexRDDVertexRDD には含まれません。
さらに、aggregateMessages はオプションの tripletsFields を取ります。これは、EdgeContext でどのデータにアクセスされるか(つまり、ソース頂点属性はアクセスするが、デスティネーション頂点属性はアクセスしない)を示します。tripletsFields の可能なオプションは TripletFields で定義されており、デフォルト値は TripletFields.All です。これは、ユーザー定義の sendMsg 関数が EdgeContext のどのフィールドにもアクセスできることを示します。tripletFields 引数は、EdgeContext の一部のみが必要であることを GraphX に通知するために使用でき、GraphX は最適化された結合戦略を選択できます。たとえば、各ユーザーのフォロワーの平均年齢を計算する場合、ソースフィールドのみが必要になるため、ソースフィールドのみが必要であることを示すために TripletFields.Src を使用します。
GraphX の以前のバージョンでは、バイトコード検査を使用して
TripletFieldsを推測していましたが、バイトコード検査はわずかに信頼性が低いことが判明したため、より明示的なユーザー制御を採用しました。
次の例では、aggregateMessages 演算子を使用して、各ユーザーのより年上のフォロワーの平均年齢を計算します。
import org.apache.spark.graphx.{Graph, VertexRDD}
import org.apache.spark.graphx.util.GraphGenerators
// Create a graph with "age" as the vertex property.
// Here we use a random graph for simplicity.
val graph: Graph[Double, Int] =
GraphGenerators.logNormalGraph(sc, numVertices = 100).mapVertices( (id, _) => id.toDouble )
// Compute the number of older followers and their total age
val olderFollowers: VertexRDD[(Int, Double)] = graph.aggregateMessages[(Int, Double)](
triplet => { // Map Function
if (triplet.srcAttr > triplet.dstAttr) {
// Send message to destination vertex containing counter and age
triplet.sendToDst((1, triplet.srcAttr))
}
},
// Add counter and age
(a, b) => (a._1 + b._1, a._2 + b._2) // Reduce Function
)
// Divide total age by number of older followers to get average age of older followers
val avgAgeOfOlderFollowers: VertexRDD[Double] =
olderFollowers.mapValues( (id, value) =>
value match { case (count, totalAge) => totalAge / count } )
// Display the results
avgAgeOfOlderFollowers.collect().foreach(println(_))
aggregateMessages操作は、メッセージ(およびメッセージの合計)が定数サイズ(例: float と加算ではなくリストと連結)の場合に最適に実行されます。
Map Reduce Triplets 移行ガイド (レガシー)
GraphX の以前のバージョンでは、近傍集計は mapReduceTriplets 演算子を使用して行われていました。
class Graph[VD, ED] {
def mapReduceTriplets[Msg](
map: EdgeTriplet[VD, ED] => Iterator[(VertexId, Msg)],
reduce: (Msg, Msg) => Msg)
: VertexRDD[Msg]
}mapReduceTriplets 演算子は、各トリプレットに適用され、ユーザー定義の reduce 関数を使用して集計される*メッセージ*を生成できるユーザー定義のマップ関数を取ります。しかし、返されるイテレータの使用は高コストであり、追加の最適化(例: ローカル頂点再番号付け)の適用を妨げることがわかりました。aggregateMessages では、トリプレットフィールドと、ソースおよびデスティネーション頂点に明示的にメッセージを送信する関数を公開する EdgeContext を導入しました。さらに、バイトコード検査を削除し、代わりにユーザーがトリプレットのどのフィールドが実際に必要かを指定するように要求しました。
次のコードブロックは mapReduceTriplets を使用しています。
val graph: Graph[Int, Float] = ...
def msgFun(triplet: Triplet[Int, Float]): Iterator[(Int, String)] = {
Iterator((triplet.dstId, "Hi"))
}
def reduceFun(a: String, b: String): String = a + " " + b
val result = graph.mapReduceTriplets[String](msgFun, reduceFun)aggregateMessages を使用して書き換えることができます。
val graph: Graph[Int, Float] = ...
def msgFun(triplet: EdgeContext[Int, Float, String]) {
triplet.sendToDst("Hi")
}
def reduceFun(a: String, b: String): String = a + " " + b
val result = graph.aggregateMessages[String](msgFun, reduceFun)次数情報の計算
一般的な集計タスクは、各頂点の次数(各頂点に隣接するエッジの数)を計算することです。有向グラフのコンテキストでは、各頂点の入次数、出次数、および合計次数を知る必要があることがよくあります。GraphOps クラスには、各頂点の次数を計算するための演算子のコレクションが含まれています。たとえば、次の例では、最大入次数、出次数、および合計次数を計算します。
// Define a reduce operation to compute the highest degree vertex
def max(a: (VertexId, Int), b: (VertexId, Int)): (VertexId, Int) = {
if (a._2 > b._2) a else b
}
// Compute the max degrees
val maxInDegree: (VertexId, Int) = graph.inDegrees.reduce(max)
val maxOutDegree: (VertexId, Int) = graph.outDegrees.reduce(max)
val maxDegrees: (VertexId, Int) = graph.degrees.reduce(max)隣接ノードの収集
場合によっては、各頂点で隣接する頂点とその属性を収集することによって計算を表現する方が簡単な場合があります。これは、collectNeighborIds および collectNeighbors 演算子を使用して簡単に実現できます。
class GraphOps[VD, ED] {
def collectNeighborIds(edgeDirection: EdgeDirection): VertexRDD[Array[VertexId]]
def collectNeighbors(edgeDirection: EdgeDirection): VertexRDD[ Array[(VertexId, VD)] ]
}これらの演算子は、情報を重複させ、かなりの通信を必要とするため、非常にコストがかかる可能性があります。可能な場合は、
aggregateMessages演算子を直接使用して同じ計算を表現してみてください。
キャッシングとアンキャッシング
Spark では、RDD はデフォルトでメモリに永続化されません。再計算を回避するには、複数回使用する際に明示的にキャッシュする必要があります(Spark プログラミングガイド を参照)。GraphX のグラフも同様です。グラフを複数回使用する場合は、まずそれに Graph.cache() を呼び出すようにしてください。
反復計算では、パフォーマンスを最適化するために*アンキャッシング*が必要になる場合もあります。デフォルトでは、キャッシュされた RDD およびグラフは、メモリ圧力が LRU 順で追い出すまでメモリに残ります。反復計算では、前のイテレーションの中間結果がキャッシュを埋めます。最終的には追い出されますが、メモリに格納されている不要なデータはガベージコレクションを遅くします。中間結果が不要になったらすぐにアンキャッシュする方が効率的です。これには、各イテレーションでグラフまたは RDD をマテリアライズ(キャッシュして強制)し、他のすべてのデータセットをアンキャッシュし、将来のイテレーションではマテリアライズされたデータセットのみを使用することが含まれます。ただし、グラフは複数の RDD で構成されているため、それらを正しくアンパースクリプトすることは困難な場合があります。反復計算には、中間結果を正しくアンパースクリプトする Pregel API を使用することをお勧めします。
Pregel API
グラフは本質的に再帰的なデータ構造です。なぜなら、頂点のプロパティは隣接頂点のプロパティに依存し、さらにその隣接頂点のプロパティに依存するからです。その結果、多くの重要なグラフアルゴリズムは、固定点条件に達するまで各頂点のプロパティを反復的に再計算します。これらの反復アルゴリズムを表現するために、さまざまなグラフ並列抽象化が提案されています。GraphX は Pregel API のバリアントを公開します。
全体として、GraphX の Pregel 演算子は、*グラフのトポロジに制約された*バルク同期並列メッセージング抽象化です。Pregel 演算子は一連のスーパーステップで実行されます。ここでは、頂点は前のスーパーステップからのインバウンドメッセージの*合計*を受信し、頂点プロパティの新しい値を計算し、次のスーパーステップで隣接頂点にメッセージを送信します。Pregel とは異なり、メッセージはエッジトリプレットの関数として並列に計算され、メッセージ計算はソースとデスティネーションの頂点属性の両方にアクセスできます。メッセージを受信しない頂点は、スーパーステップ内でスキップされます。Pregel 演算子は、メッセージが残っていない場合に反復を終了し、最終的なグラフを返します。
標準的な Pregel 実装とは異なり、GraphX の頂点は隣接頂点にのみメッセージを送信でき、メッセージの構築はユーザー定義のメッセージング関数を使用して並列に行われることに注意してください。これらの制約により、GraphX 内で追加の最適化が可能になります。
以下は、Pregel 演算子の型シグネチャと、その実装の*スケッチ*です(注意: 長いリネージチェーンによる stackOverflowError を回避するために、pregel は「spark.graphx.pregel.checkpointInterval」を正の数(例: 10)に設定してグラフとメッセージを定期的にチェックポイントします。また、SparkContext.setCheckpointDir(directory: String) を使用してチェックポイントディレクトリも設定します)。
class GraphOps[VD, ED] {
def pregel[A]
(initialMsg: A,
maxIter: Int = Int.MaxValue,
activeDir: EdgeDirection = EdgeDirection.Out)
(vprog: (VertexId, VD, A) => VD,
sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexId, A)],
mergeMsg: (A, A) => A)
: Graph[VD, ED] = {
// Receive the initial message at each vertex
var g = mapVertices( (vid, vdata) => vprog(vid, vdata, initialMsg) ).cache()
// compute the messages
var messages = GraphXUtils.mapReduceTriplets(g, sendMsg, mergeMsg)
var activeMessages = messages.count()
// Loop until no messages remain or maxIterations is achieved
var i = 0
while (activeMessages > 0 && i < maxIterations) {
// Receive the messages and update the vertices.
g = g.joinVertices(messages)(vprog).cache()
val oldMessages = messages
// Send new messages, skipping edges where neither side received a message. We must cache
// messages so it can be materialized on the next line, allowing us to uncache the previous
// iteration.
messages = GraphXUtils.mapReduceTriplets(
g, sendMsg, mergeMsg, Some((oldMessages, activeDirection))).cache()
activeMessages = messages.count()
i += 1
}
g
}
}Pregel は 2 つの引数リスト(つまり、graph.pregel(list1)(list2))を取ることに注意してください。最初の引数リストには、初期メッセージ、最大反復回数、およびメッセージを送信するエッジの方向(デフォルトではアウトエッジに沿って)などの構成パラメータが含まれています。2 番目の引数リストには、メッセージの受信(頂点プログラム vprog)、メッセージの計算(sendMsg)、およびメッセージの結合 mergeMsg のためのユーザー定義関数が含まれています。
Pregel 演算子を使用して、次の例のような単一ソース最短経路などの計算を表現できます。
import org.apache.spark.graphx.{Graph, VertexId}
import org.apache.spark.graphx.util.GraphGenerators
// A graph with edge attributes containing distances
val graph: Graph[Long, Double] =
GraphGenerators.logNormalGraph(sc, numVertices = 100).mapEdges(e => e.attr.toDouble)
val sourceId: VertexId = 42 // The ultimate source
// Initialize the graph such that all vertices except the root have distance infinity.
val initialGraph = graph.mapVertices((id, _) =>
if (id == sourceId) 0.0 else Double.PositiveInfinity)
val sssp = initialGraph.pregel(Double.PositiveInfinity)(
(id, dist, newDist) => math.min(dist, newDist), // Vertex Program
triplet => { // Send Message
if (triplet.srcAttr + triplet.attr < triplet.dstAttr) {
Iterator((triplet.dstId, triplet.srcAttr + triplet.attr))
} else {
Iterator.empty
}
},
(a, b) => math.min(a, b) // Merge Message
)
println(sssp.vertices.collect().mkString("\n"))グラフビルダー
GraphX は、RDD の頂点とエッジのコレクション、またはディスクからグラフを構築するためのいくつかの方法を提供します。グラフビルダーはいずれもデフォルトでグラフのエッジを再パーティション分割しません。代わりに、エッジはデフォルトのパーティション(HDFS の元のブロックなど)に残されます。Graph.groupEdges は、グラフが再パーティション分割されていることを前提としています。なぜなら、同一のエッジが同じパーティションに配置されていることを前提としているため、groupEdges を呼び出す前に Graph.partitionBy を呼び出す必要があります。
object GraphLoader {
def edgeListFile(
sc: SparkContext,
path: String,
canonicalOrientation: Boolean = false,
minEdgePartitions: Int = 1)
: Graph[Int, Int]
}GraphLoader.edgeListFile は、ディスク上のエッジのリストからグラフをロードする方法を提供します。これは、次のような形式の(ソース頂点 ID、デスティネーション頂点 ID)ペアの隣接リストを解析し、# で始まるコメント行をスキップします。
# This is a comment
2 1
4 1
1 2
指定されたエッジから Graph を作成し、エッジによって参照される頂点を自動的に作成します。すべての頂点とエッジの属性はデフォルトで 1 になります。canonicalOrientation 引数により、エッジを正の方向(srcId < dstId)に再方向付けできます。これは、連結成分アルゴリズムで必要です。minEdgePartitions 引数は、生成される最小エッジパーティション数を指定します。たとえば、HDFS ファイルに複数のブロックがある場合など、指定された数よりも多いエッジパーティションが存在する可能性があります。
object Graph {
def apply[VD, ED](
vertices: RDD[(VertexId, VD)],
edges: RDD[Edge[ED]],
defaultVertexAttr: VD = null)
: Graph[VD, ED]
def fromEdges[VD, ED](
edges: RDD[Edge[ED]],
defaultValue: VD): Graph[VD, ED]
def fromEdgeTuples[VD](
rawEdges: RDD[(VertexId, VertexId)],
defaultValue: VD,
uniqueEdges: Option[PartitionStrategy] = None): Graph[VD, Int]
}Graph.apply は、頂点およびエッジの RDD からグラフを作成できます。重複する頂点は任意に選択され、エッジ RDD に存在するが頂点 RDD に存在しない頂点にはデフォルト属性が割り当てられます。
Graph.fromEdges は、エッジの RDD のみからグラフを作成できるようにし、エッジによって参照される頂点を自動的に作成してデフォルト値を割り当てます。
Graph.fromEdgeTuples は、エッジタプルの RDD のみからグラフを作成できるようにし、エッジに値 1 を割り当て、エッジによって参照される頂点を自動的に作成してデフォルト値を割り当てます。また、エッジの重複排除もサポートしています。重複排除するには、uniqueEdges パラメータとして(たとえば、Some の PartitionStrategy を)渡します(例: uniqueEdges = Some(PartitionStrategy.RandomVertexCut))。パーティション戦略は、同一のエッジを同じパーティションに配置して重複排除できるようにするために必要です。
頂点およびエッジ RDD
GraphX は、グラフ内に格納されている頂点とエッジの RDD ビューを公開します。しかし、GraphX は頂点とエッジを最適化されたデータ構造に保持し、これらのデータ構造が追加機能を提供するため、頂点とエッジはそれぞれ VertexRDDVertexRDD および EdgeRDDEdgeRDD として返されます。このセクションでは、これらの型の追加の便利な機能のいくつかをレビューします。これは不完全なリストであり、操作の公式リストについては API ドキュメントを参照してください。
VertexRDD
VertexRDD[A] は RDD[(VertexId, A)] を拡張し、各 VertexId が*1 回のみ*出現するという追加の制約を課します。さらに、VertexRDD[A] は、それぞれ型 A の属性を持つ頂点の*セット*を表します。内部的には、これは頂点属性を再利用可能なハッシュマップデータ構造に格納することによって実現されます。その結果、2 つの VertexRDD が同じベース VertexRDDVertexRDD から派生した場合(例: filter または mapValues による)、ハッシュ評価なしで定数時間で結合できます。このインデックス付きデータ構造を活用するために、VertexRDDVertexRDD は次の追加機能を提供します。
class VertexRDD[VD] extends RDD[(VertexId, VD)] {
// Filter the vertex set but preserves the internal index
def filter(pred: Tuple2[VertexId, VD] => Boolean): VertexRDD[VD]
// Transform the values without changing the ids (preserves the internal index)
def mapValues[VD2](map: VD => VD2): VertexRDD[VD2]
def mapValues[VD2](map: (VertexId, VD) => VD2): VertexRDD[VD2]
// Show only vertices unique to this set based on their VertexId's
def minus(other: RDD[(VertexId, VD)])
// Remove vertices from this set that appear in the other set
def diff(other: VertexRDD[VD]): VertexRDD[VD]
// Join operators that take advantage of the internal indexing to accelerate joins (substantially)
def leftJoin[VD2, VD3](other: RDD[(VertexId, VD2)])(f: (VertexId, VD, Option[VD2]) => VD3): VertexRDD[VD3]
def innerJoin[U, VD2](other: RDD[(VertexId, U)])(f: (VertexId, VD, U) => VD2): VertexRDD[VD2]
// Use the index on this RDD to accelerate a `reduceByKey` operation on the input RDD.
def aggregateUsingIndex[VD2](other: RDD[(VertexId, VD2)], reduceFunc: (VD2, VD2) => VD2): VertexRDD[VD2]
}たとえば、filter 演算子が VertexRDDVertexRDD を返すことに注意してください。Filter は実際には BitSet を使用して実装されており、インデックスを再利用して、他の VertexRDD との高速結合の能力を維持します。同様に、mapValues 演算子では、map 関数が VertexId を変更できないため、同じ HashMap データ構造を再利用できます。 leftJoin と innerJoin は、同じ HashMap から派生した 2 つの VertexRDD を結合するときを識別し、コストのかかるポイントルックアップではなく線形スキャンによって結合を実装できます。
aggregateUsingIndex 演算子は、RDD[(VertexId, A)] から新しい VertexRDDVertexRDD を効率的に構築するのに役立ちます。概念的には、ある RDD[(VertexId, A)] の*スーパーセット*である頂点のセット over VertexRDD[B] を構築した場合、インデックスを再利用して、RDD[(VertexId, A)] を集計してからインデックス付けできます。たとえば。
val setA: VertexRDD[Int] = VertexRDD(sc.parallelize(0L until 100L).map(id => (id, 1)))
val rddB: RDD[(VertexId, Double)] = sc.parallelize(0L until 100L).flatMap(id => List((id, 1.0), (id, 2.0)))
// There should be 200 entries in rddB
rddB.count
val setB: VertexRDD[Double] = setA.aggregateUsingIndex(rddB, _ + _)
// There should be 100 entries in setB
setB.count
// Joining A and B should now be fast!
val setC: VertexRDD[Double] = setA.innerJoin(setB)((id, a, b) => a + b)EdgeRDD
EdgeRDD[ED] は RDD[Edge[ED]] を拡張し、PartitionStrategy で定義されたさまざまなパーティショニング戦略のいずれかを使用してブロックにエッジを編成します。各パーティション内では、エッジ属性と隣接構造は別々に格納されており、属性値が変更されるときに最大限の再利用が可能になります。
公開されている 3 つの追加関数は EdgeRDDEdgeRDD によって提供されます。
// Transform the edge attributes while preserving the structure
def mapValues[ED2](f: Edge[ED] => ED2): EdgeRDD[ED2]
// Reverse the edges reusing both attributes and structure
def reverse: EdgeRDD[ED]
// Join two `EdgeRDD`s partitioned using the same partitioning strategy.
def innerJoin[ED2, ED3](other: EdgeRDD[ED2])(f: (VertexId, VertexId, ED, ED2) => ED3): EdgeRDD[ED3]ほとんどのアプリケーションでは、EdgeRDDEdgeRDD に対する操作は、グラフ演算子を通じて達成されるか、または基盤となる RDD クラスで定義された操作に依存することがわかっています。
最適化された表現
GraphX での分散グラフの表現で使用される最適化の詳細な説明は、このガイドの範囲を超えていますが、高レベルの理解は、スケーラブルなアルゴリズムの設計と API の最適な使用に役立ちます。GraphX は、分散グラフパーティショニングに頂点カットアプローチを採用しています。
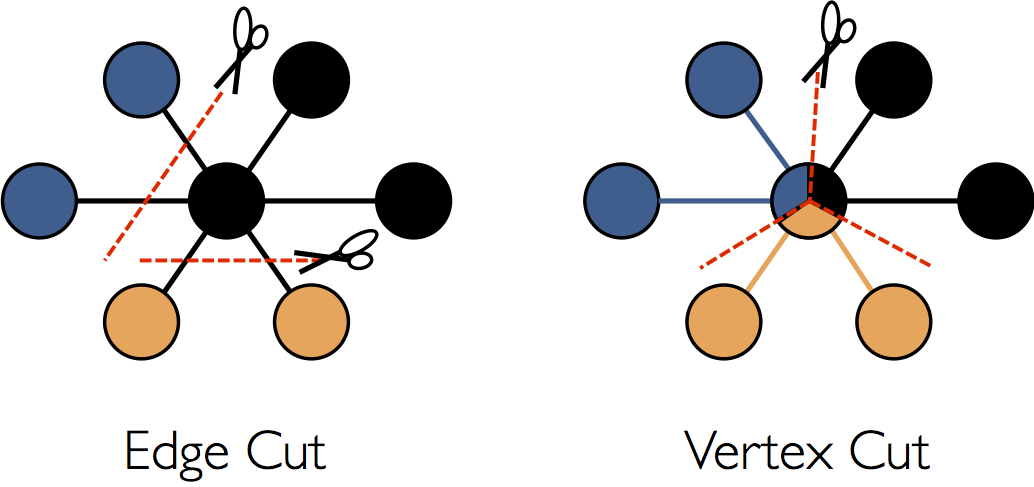
エッジに沿ってグラフを分割するのではなく、GraphX は頂点に沿ってグラフをパーティション分割し、通信とストレージのオーバーヘッドの両方を削減できます。論理的には、これはエッジをマシンに割り当て、頂点が複数のマシンにまたがることを可能に対応します。エッジを割り当てる正確な方法は、PartitionStrategy に依存し、さまざまなヒューリスティックにはいくつかのトレードオフがあります。ユーザーは、Graph.partitionBy 演算子を使用してグラフを再パーティション分割することによって、さまざまな戦略を選択できます。デフォルトのパーティショニング戦略は、グラフ構築時に提供されるエッジの初期パーティショニングを使用することです。ただし、ユーザーは 2D パーショニングや GraphX に含まれる他のヒューリスティックに簡単に切り替えることができます。
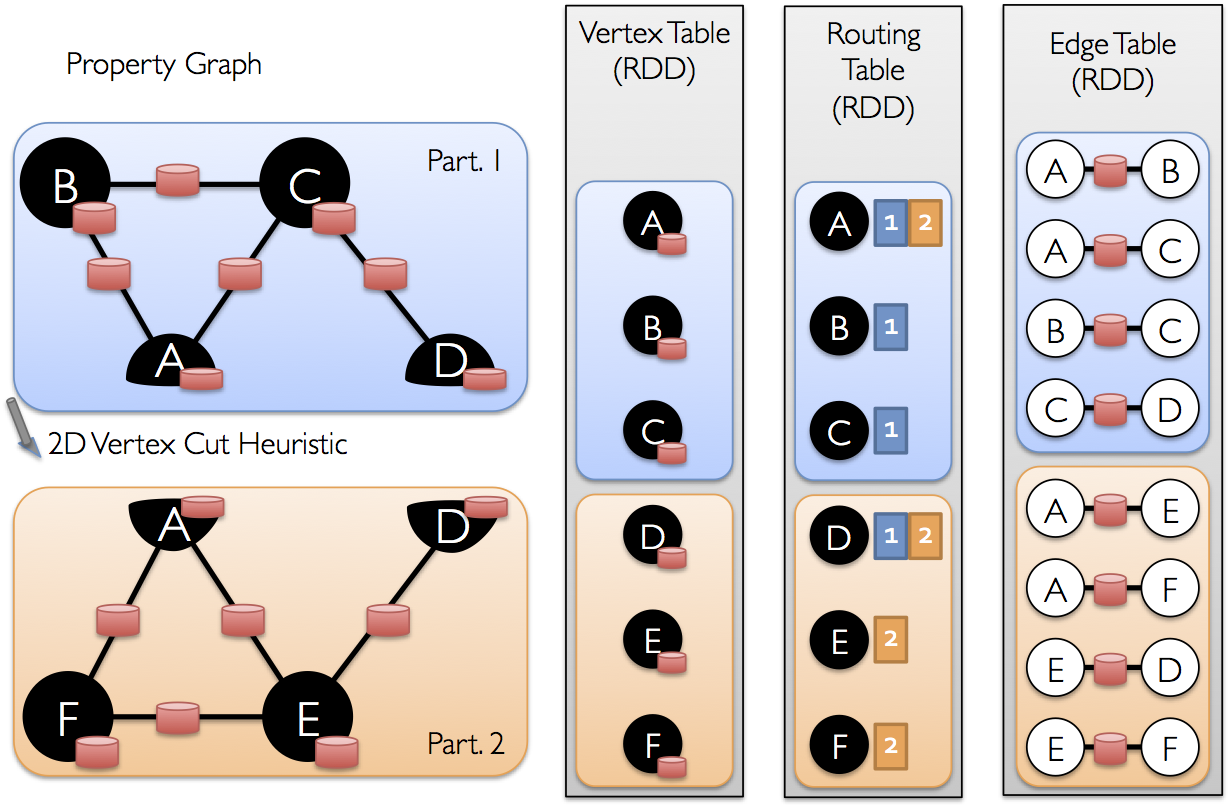
エッジがパーティション分割されたら、効率的なグラフ並列計算の主な課題は、頂点属性とエッジを効率的に結合することです。現実世界のグラフは通常、頂点よりもエッジが多いため、頂点属性をエッジに移動します。すべてのパーティションにすべての頂点に隣接するエッジが含まれるわけではないため、triplets や aggregateMessages のような操作に必要な頂点をブロードキャストする場所を特定するルーティングテーブルを内部的に維持します。
グラフアルゴリズム
GraphX には、分析タスクを簡略化するためのグラフアルゴリズムのセットが含まれています。アルゴリズムは org.apache.spark.graphx.lib パッケージに含まれており、GraphOps を介して Graph のメソッドとして直接アクセスできます。このセクションでは、アルゴリズムとその使用方法について説明します。
PageRank
PageRank は、グラフ内の各頂点の重要度を測定します。ここでの仮定は、*u* から *v* へのエッジは *v* の重要度に対する *u* による承認を表すということです。たとえば、Twitter ユーザーが多くの他のユーザーにフォローされている場合、そのユーザーは高くランク付けされます。
GraphX には、PageRank オブジェクト のメソッドとして、PageRank の静的および動的実装が付属しています。静的 PageRank は固定数の反復で実行されますが、動的 PageRank はランクが収束するまで(つまり、指定された許容誤差よりも変化しなくなるまで)実行されます。GraphOps を使用すると、これらのアルゴリズムを Graph のメソッドとして直接呼び出すことができます。
GraphX には、PageRank を実行できるソーシャルネットワークのサンプルデータセットも含まれています。ユーザーのセットは data/graphx/users.txt に、ユーザー間の関係のセットは data/graphx/followers.txt にあります。次のように、各ユーザーの PageRank を計算します。
import org.apache.spark.graphx.GraphLoader
// Load the edges as a graph
val graph = GraphLoader.edgeListFile(sc, "data/graphx/followers.txt")
// Run PageRank
val ranks = graph.pageRank(0.0001).vertices
// Join the ranks with the usernames
val users = sc.textFile("data/graphx/users.txt").map { line =>
val fields = line.split(",")
(fields(0).toLong, fields(1))
}
val ranksByUsername = users.join(ranks).map {
case (id, (username, rank)) => (username, rank)
}
// Print the result
println(ranksByUsername.collect().mkString("\n"))連結成分
連結成分アルゴリズムは、グラフの各連結成分を、その最小番号の頂点の ID でラベル付けします。たとえば、ソーシャルネットワークでは、連結成分はクラスターを近似できます。GraphX には、ConnectedComponents オブジェクト にアルゴリズムの実装が含まれており、PageRank セクションのソーシャルネットワークのサンプルデータセットの連結成分を次のように計算します。
import org.apache.spark.graphx.GraphLoader
// Load the graph as in the PageRank example
val graph = GraphLoader.edgeListFile(sc, "data/graphx/followers.txt")
// Find the connected components
val cc = graph.connectedComponents().vertices
// Join the connected components with the usernames
val users = sc.textFile("data/graphx/users.txt").map { line =>
val fields = line.split(",")
(fields(0).toLong, fields(1))
}
val ccByUsername = users.join(cc).map {
case (id, (username, cc)) => (username, cc)
}
// Print the result
println(ccByUsername.collect().mkString("\n"))三角形カウント
頂点が 2 つの隣接する頂点とそれらの間にエッジがある場合、その頂点は三角形の一部です。GraphX は、TriangleCount オブジェクト に三角形カウントアルゴリズムを実装しています。これは、各頂点を通る三角形の数を決定し、クラスタリングの尺度を提供します。ソーシャルネットワークデータセットの三角形カウントを、PageRank セクションから計算します。*注意: TriangleCount は、エッジが標準的な順序(srcId < dstId)であり、グラフが Graph.partitionBy を使用してパーティション分割されている必要があることに注意してください。*
import org.apache.spark.graphx.{GraphLoader, PartitionStrategy}
// Load the edges in canonical order and partition the graph for triangle count
val graph = GraphLoader.edgeListFile(sc, "data/graphx/followers.txt", true)
.partitionBy(PartitionStrategy.RandomVertexCut)
// Find the triangle count for each vertex
val triCounts = graph.triangleCount().vertices
// Join the triangle counts with the usernames
val users = sc.textFile("data/graphx/users.txt").map { line =>
val fields = line.split(",")
(fields(0).toLong, fields(1))
}
val triCountByUsername = users.join(triCounts).map { case (id, (username, tc)) =>
(username, tc)
}
// Print the result
println(triCountByUsername.collect().mkString("\n"))例
テキストファイルからグラフを構築し、グラフを重要な関係とユーザーに制限し、サブグラフでページランクを実行し、最後にトップユーザーに関連付けられた属性を返す必要があるとします。GraphX を使用すると、これをわずか数行で行うことができます。
import org.apache.spark.graphx.GraphLoader
// Load my user data and parse into tuples of user id and attribute list
val users = (sc.textFile("data/graphx/users.txt")
.map(line => line.split(",")).map( parts => (parts.head.toLong, parts.tail) ))
// Parse the edge data which is already in userId -> userId format
val followerGraph = GraphLoader.edgeListFile(sc, "data/graphx/followers.txt")
// Attach the user attributes
val graph = followerGraph.outerJoinVertices(users) {
case (uid, deg, Some(attrList)) => attrList
// Some users may not have attributes so we set them as empty
case (uid, deg, None) => Array.empty[String]
}
// Restrict the graph to users with usernames and names
val subgraph = graph.subgraph(vpred = (vid, attr) => attr.size == 2)
// Compute the PageRank
val pagerankGraph = subgraph.pageRank(0.001)
// Get the attributes of the top pagerank users
val userInfoWithPageRank = subgraph.outerJoinVertices(pagerankGraph.vertices) {
case (uid, attrList, Some(pr)) => (pr, attrList.toList)
case (uid, attrList, None) => (0.0, attrList.toList)
}
println(userInfoWithPageRank.vertices.top(5)(Ordering.by(_._2._1)).mkString("\n"))